Der Satz des Pythagoras ist nicht von Pythagoras: Babylonische Tafel mit denselben Berechnungen 1000 Jahre früher entdeckt

Jeder kennt den so genannten Satz des Pythagoras aus seiner Schulzeit, der feierlich besagt: "In einem rechtwinkligen Dreieck ist das auf der Hypotenuse konstruierte Quadrat gleich der Summe der auf den Kathexen konstruierten Quadrate." Man kann sich fast vorstellen, dass Pythagoras selbst diesen Satz zum ersten Mal rezitierte und ihn dann an seine Schüler in seiner geheimen Schule weitergab.
Doch die jüngste Entdeckung einer babylonischen Tafel stellt alles in Frage: Die Tafel, auf der die logische Begründung des Satzes von Pythagoras genau angegeben ist, wird weit vor seiner Geburt datiert.
Der von den Babyloniern verwendete Satz des Pythagoras, 1000 Jahre früher
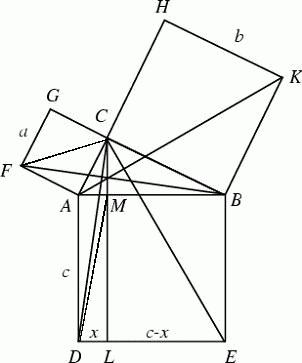
Die Tafel trägt die Bezeichnung Si.427 und besteht aus Ton: Auf ihr befinden sich zahlreiche Keilschriftzeichen in Quadraten. Wissenschaftlern und Archäologen ist es gelungen, diese einfachen mathematischen Berechnungen in die von den Babyloniern verwendete Sexagesimalbasis zu übersetzen und den Satz des Pythagoras zweifelsfrei zu erkennen.
Wie haben die Babylonier den Satz verwendet?
Die Tafel diente dazu, dem "Leser" beizubringen, wie man exakte rechtwinklige Dreiecke ableitet, um eindeutige Grenzen auf Feldern zu ziehen. Der Satz des Pythagoras findet in der Tat auch in der Architektur und im Bauwesen Anwendung, da er zur Berechnung der Länge der Diagonale eines Rechtecks oder allgemeiner der Länge der Diagonale, die zwei gerade Linien verbindet, verwendet werden kann.
Entdeckung der babylonischen Tafel

Die kugelförmige, handtellergroße Tontafel wurde im Rahmen einer französischen archäologischen Expedition entdeckt und wird auf die Zeit zwischen 1900 und 1600 v. Chr. datiert. Sie befindet sich heute im Archäologischen Museum in Istanbul. Die Datierung macht deutlich, dass die Kenntnis des Satzes schon vor Pythagoras und seiner Geburt bekannt war.
Warum ist er als Satz des Pythagoras in die Geschichte eingegangen?
Der Grund dafür, dass der fundamentale Satz der euklidischen Geometrie diesen Namen trägt, liegt einfach darin, dass die Quellen nicht berücksichtigt werden. Die Vorlesungen von Pythagoras und seinen anderen Lehrern derselben Schule wurden fast ausschließlich mündlich gehalten, und die Weitergabe von Ohr zu Ohr könnte im Laufe der Zeit die Spuren des Ursprungs des Satzes verwischt haben.
Die Popularität der Schule des Pythagoras, das Geheimnis und die Faszination seiner Biografie haben nur dazu beigetragen, die Aufmerksamkeit auf seine Person zu lenken, so dass man glaubt, der Satz von den Dreiecken und Quadraten stamme von seiner Hand.
Sollten wir aufhören, den Satz des Pythagoras so zu nennen?

Das Verdienst von Pythagoras und seinen Anhängern ist unbestreitbar: Sie haben den Satz des Pythagoras populär gemacht und zu seiner praktischen Anwendung beigetragen, so dass er auch heute noch die Grundlage für zahlreiche Berechnungen in verschiedenen Bereichen bildet, von der Architektur bis zur Navigation über die einfache Geometrie.
Es ist also nicht ganz falsch, sich weiterhin auf den Satz des Pythagoras zu beziehen, schließlich wäre es nicht das erste Mal, dass eine Entdeckung nach der Person benannt wird, die sie populär gemacht hat, und nicht nach ihrem Erfinder. In jedem Fall ist die Kenntnis des wahren Ursprungs des Satzes von Pythagoras sowohl für die allgemeine Kultur als auch für Cäsar - oder die Babylonier - wünschenswert.